公园道路设计的模型 45页

安康学院第四届数学建模竞赛承诺书我们仔细阅读了安康学院数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研宄、讨论与赛题有关的问题。我们知道，抄袭别人的成果是违反竞赛规则的，如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。如有违反竞赛规则的行为，我们将受到严肃处理。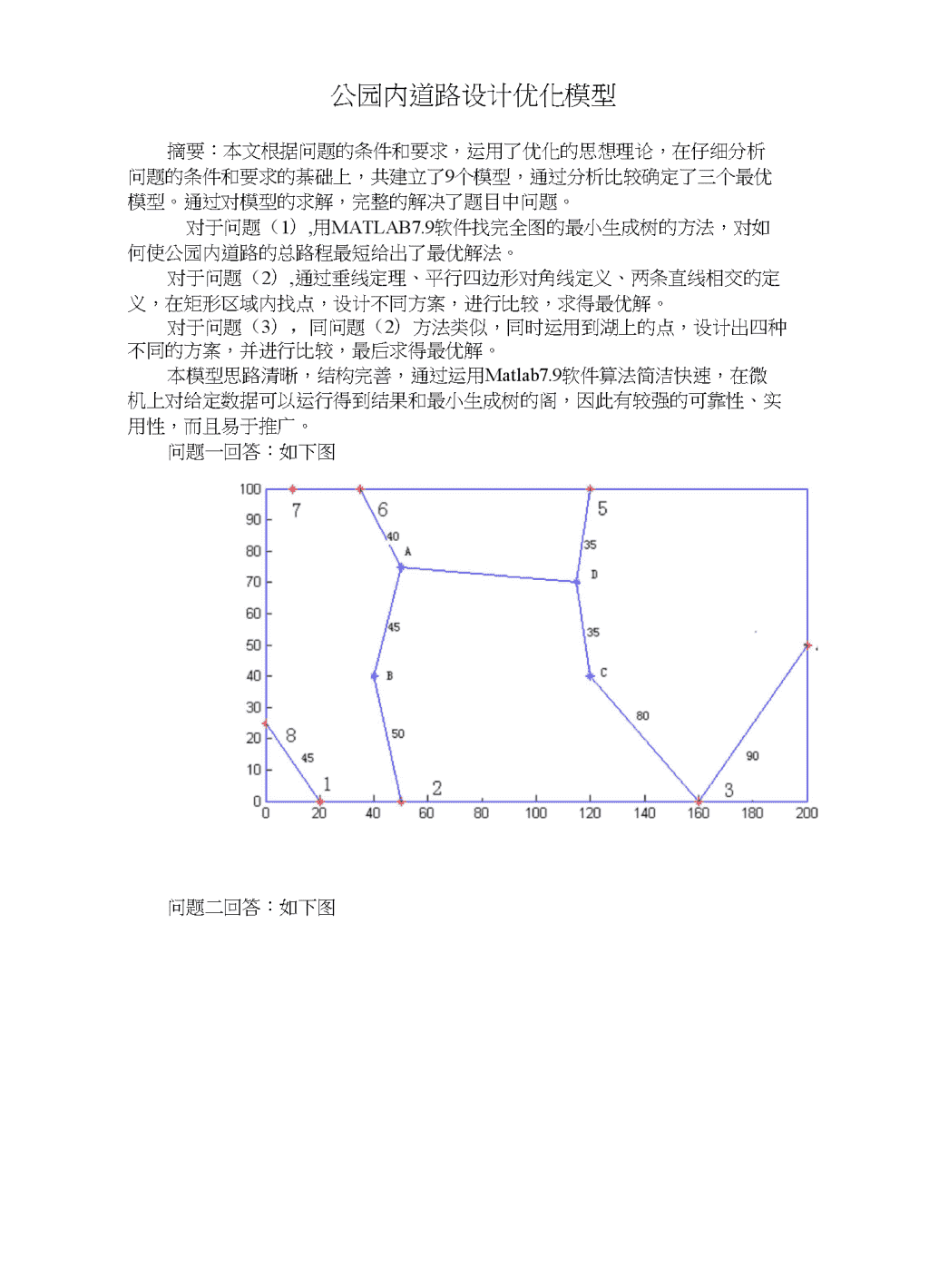我们参赛选择的题号是（从A/B中选择一项填写）：B题我们的参赛报名号为（如果赛区设置报名号的话）：120445所属院系（请填写完整的全名）：数学系参赛队员（打印并签名）：1.«2.何荟明3.路杨利指导教师或指导教师组负责人（打印并签名）：刘铁武海辉日期：2012年5月2日 安康学院第四届数学建模竞赛编号专用页评阅编号:评阅记录:评阅人评分备注 公园内道路设计优化模型摘要：本文根据问题的条件和要求，运用了优化的思想理论，在仔细分析问题的条件和要求的棊础上，共建立了9个模型，通过分析比较确定了三个最优模型。通过对模型的求解，完整的解决了题目中问题。对于问题（1）,用MATLAB7.9软件找完全图的最小生成树的方法，对如何使公园内道路的总路程最短给出了最优解法。对于问题（2）,通过垂线定理、平行四边形对角线定义、两条直线相交的定义，在矩形区域内找点，设计不同方案，进行比较，求得最优解。对于问题（3），同问题（2）方法类似，同时运用到湖上的点，设计出四种不同的方案，并进行比较，最后求得最优解。本模型思路清晰，结构完善，通过运用Matlab7.9软件算法简洁快速，在微机上对给定数据可以运行得到结果和最小生成树的阁，因此有较强的可靠性、实用性，而且易于推广。问题一回答：如下图问题二回答：如下图 问题三冋答：如下图30•»3010•I«w.,....p.o1—t>-■，*一▲AJ4：h0X)O60»100IXIO1601助JOO关键词：道路设计完全图最小生成树优化模型一、问题重述四安某大学计划建一个形状为矩形或其他不规则阁形的公园，不仅为了美化校园环境，也是想为其学生提供更好的生活条件。公园计划有若干个入口，现在你需要建立一个模型去设计道路让任意两个入口相连（可以利用公园四周的边，即默认矩形的四条边上存在已经建好的道路，此道路不计入道路总长），使总的道路长度和最小，前提要求是任意的两个入口之间的最短道路长不人于两点连线的1.4倍。 主要设计对象可假设为如图所示的矩形公园，其相关数据为：长200米，宽 100米，1至8各入口的坐标分别为：P1(20,0)，P2(50,0)，P3(160,0)，P4(200,50)，P5(120,100),P6(35,l00),P7(10,l00)，P8(0,25).示意图见图1，其中图2即是一种满足要求的设计，但不是最优的。现完成以下问题：问题一：假定公园内确定要使用4个道路交叉点为：A(50,75),B(40,40),C(120,40),D(115,70)。问如何设计道路可使公园内道路的总路程最短。建立模型并给出算法。画出道路设计，计算新修路的总路程。问题二：现在公园内可以任意修建道路，如何在满足条件下使总路程最少。建立模型并给出算法。给出道路交叉点的坐标，岡出道路设计，计算新修路的总路程。问题三：若公园内有一条矩形的湖，新修的道路不能通过，但可以到达湖四周的边，示意图见图3。重复完成问题二的任务。其中矩形的湖为Rl(140,70)，R2(140,45)，R3=(165,45)，R4=(165,70)。10090807060图1公园及入口示意40 3020100020406080100120140160180200 2一种可能的道路设计10090807060504030201000204060801001201401601802003有湖的示意图二、符号说明 3、sparse稀疏矩阵5、full普通矩阵4、graphminspantree在聞中找最小生成树6、treelength最小生成树的长度7、sum求和8、~一一任意两点之间的距离9、view画出图形10、顶点集11、G=(P.E.W)赋权图12.W=（wij）^一一邻接矩阵13、pred权14、表中P9、P10、Pll、P12——点A、B、C、D三、模型假设1.假设其公园内的地质都一样，即在公园内任意地点处修路没有阻碍;2.所给的坐标点基本上真实准确。、问题分析本问题难点是要同时考虑到公园任意的两个入口之间的最短道路长不大于两点连线的1.4倍，修建的公园内部道路最短，公园内部点的位置的不确定性等因素。问题的第一问中内部的点是确定的，连接各点可构成一个完全图，利用Matlab（7.9版）编程可求得各边的权值。如梁找到这个完全图的最小生成树，并>1.满足公园任意的两个入U之间的最短道路长大于两点连线的1.4倍这一约朿条件，即可得到公园的道路最短，然后减去最小生成树中包括已建好的道路，从而得到总的公园内道路最短。即得到最优解。问题二和问题三中，如果确定了点，通过上面的分析也可得到最优解。五、模型建立与求解模型I点的坐标数据表一p（J，j、piPP3P4P5P6P7P8ABCDXi2050160200120351005040120115yj000501001001002575404070对于问题（1），先考虑简单的问题，即考虑已确定点的最优连线问题。己知12个点的坐标（见表一）。构造各边的权值为dy=xj-|+yj-yj,（/y,/,y=1,2,...,12）其屮U/，为第/个点的坐标。J 然后以P={pvpv...pn}作为顶点集，构造赋权阁G=（P，E，VV）,这里VV=（u^）i2xi2为邻接矩阵，其中％=&，/,）=1,2，...12。求公闻道路的总路程最短的问题实际上就是求图G的最小生成树问题。利用Matlab7.9版程序求解（编写程序及运行结果见附录1），得最小生成树见下图，总路程为545米，然后用总路程减去最小生成树中己建好的道路，从而得到公园内部总的道路长度和最小，即最优解为355米。模型II对于问题（2），由于问题（1）中在矩形内部设置了4个点，因此我们联想到在矩形内部设丫1个，2个，3个，4个点的模型方案。首先，连接，过点p4作p3p5的垂线于点C，由垂线段最短（垂线定理），即找到C点。连接p7，p2,由点p3，/?5，/?7，/72得到平行四边形p3p5p2＞连接对角线交于点B（平行四边形对角线定义），即找到B点。最后连接P|，p6,线段PlP6，P7P2相交于一点A，（两条直线相交的定义），即找到A点。利用Matlab程序（编写程序见附录2）求得A点、B点、C点的坐标分表为：（310/11,600/11）,（3490/39,2200/39）,（182.76,56.9）根据找到的点设计不同方案，具体方案如下，然后对各方案进行比较，求得最优解。第一种方案：点的坐标数据表二piP2P3P4P5P6P7P8BXi205016020012035100310/11yj0005010010010025600/11内部一个交点，即找到确定的点B,己知9个点的坐标（见表二）。构造各边的权值为心=xj--v/|+卜厂）1，（"•*./，’•，y=1,2,...,9）其中（U/）为第冲点的坐标。然后以^={0，/^，.../%}作为顶点集，构造赋权图G=（P，£，W），这里w=（Wy）^为邻接矩阵，其中~=dij，i，j=1，2,...9。求公园道路的总路程最短的 问题实际上就是求图G的最小生成树问题。利用Matlab7.9版程序求解（编写程序及运行结果见附录3）,通过分析最小生成树的图，显然这种方案不符合题屮要求，即可排除这种方案。第二种方案：点的坐标数据表三p(hj)piP2P3P4P5P6P7P8ACXi205016020012035100310/113490/39yj0005010010010025600/112200/39内部两个交点，即找到确定的点A、C,己知10个点的坐标（见表三）。构造各边的权值为〜=xj-X；|+yj-yj,（/y,/,j=1,2,...,10）其屮U/，"为第/个点的坐标。然后以P={/?,,p2，../?10}作为顶点集，构造赋权图G=（P，£,W）,这里vv=（wzy）iox|（）为邻接矩阵，其中~=人，/，7=1，2，...10。求公园道路的总路程最短的问题实际上就是求图G的最小生成树问题。利用Matlab7.9版程序求解（编写程序及运行结果见附录4），得到总路程为504.6552米，然后用总路程减去最小生成树中已建好的道路，从而得到公园内部总的道路长度和最小，即最优解为319.6552米。第三种方案：点的坐标数据表四P(hj)piP2P3P4P5P6P7P8ABCXi205016020012035100310/113490/39182.76y./0005010010010025600/112200/3956.9内部有三个交点，即找到确定的点A、B、C,已知11个点的坐标（见表四）。构造各边的权值为dy=xj-^|+|y厂〉71，（’巧，’，y=1，2,…，11）其中（UP为第i个点的坐标。 然后以作为顶点集，构造赋权阁G=（P，E，IV），这里VV=（H^）11X11为邻接矩阵，其中w=A，f，J=l，2，...ll。求公园道路的总路程最短的问题实际上就是求图G的最小生成树问题。利用Matlab7.9版程序求解（编写程序及运行结果见附录5），得到总路程为544.8237米，然后用总路程减去最小生成树中已建好的道路，从而得到公园内部总的道路长度和最小，即最优解为444.8237米。四种方此方案的建立与求解与模型I的过程相同。通过比较以上四种方案,得知第二种方案为最优方案。其最小生成树见下图，公园内部总的道路长度和最小，即最优解为319.6552米。57.7273/52-2727Node725Node6851X1X105.862Node5Node3Node4模型m对于问题（3），通过对问题（2）的分析，点C要经过湖面，因此排除点C。利用到上题所求出的A、B两点，同吋再运用到湖面上的点，一共是六个点，分别设计了不同的方案，进行比较，求得最优解。第一种方案：点的坐标数据表五P（i，j）piP2P3P4P5P6P7P8AR2R3Xi205016020012035100310/11140165yj0005010010010025600/114545 内部有三个交点，即找到确定的点A和湖面上的R2、R3，己知11个点的坐标（见表五）。构造各边的权值为dy=xj-Xj+yj-yj，（/j,i，j=1，2，...，11）其中为第i个点的坐标。然后以作为顶点集，构造赋权图G=（P，£，W）,这里w=（wz；/）iixii为邻接矩阵，其屮叫0=心•人j=mio求公园道路的总路程最短的问题实际上就是求图G的最小生成树问题。利用Matlab7.9版程序求解（编写程序及运行结果见附录6），得到总路程为485米，然后用总路程减去最小生成树中已建好的道路和湖边的路，从而得到公园内部总的道路长度和最小，即最优解为275米。第二种方案：p(hj)piP2P3P4P5P6P7P8ABR2Xi205016020012035100310/113490/39140yj0005010010010025600/112200/3945点的坐标数据表六内部有四个交点，即找到确定的点A、B和湖面上的R2、R3，己知12个点R316545的坐标（见表六）。构造各边的权值为其中（U，p为第i个点的坐标。然后以P=[pvp2^pn]作为顶点集，构造赋权图G=（P,£,W）,这里w=（m^）i2x12为邻接矩阵，其中~=^,/,y=l，2，...12。求公园道路的总路程最短的问题实际上就是求图G的最小生成树问题。利用Matlab7.9版程序求解（编写程序及运行结果见附录7）,得到总路程为524.1958米，然后用总路程减去最小生成树中已建好的道路和湖边的路，从而得到公园内部总的道路长度和最小，即最优解为399.1958米。第三种方案：P(U)piP2P3P4P5P6P7P8ABR2Xi205016020012035100310/113490/39140yj0005010010010025600/112200/3945点的坐标数据表七R114070R316545 P(“j)piP2P3P4P5P6P7P8ABR1Xi205016020012035100310/113490/39140yj0005010010010025600/112200/3970点的坐标数据表八闪部有五个交点，有两种情况：第一种情况找到确定的点A、B和湖面上的Rl、R2、R3,第二种情况找到确定的点A、B和湖而上的Rl、R4、R3，己知两种情况的13个点的坐标（分别见表七和表八）。构造各边的权值力R4R31651657045yj-yi其中（X/O7/）为第z个点的坐标然后以P=｛pvpy.p｝3｝作为顶点集，构造赋权阁G=（P,£，MQ，这里W=（w（/）i3xi3为邻接矩阵，其中~=1，2，...13。求公园道路的总路程最短的问题实际上就是求图G的最小生成树问题。利用Matlab7.9版程序求解（两种情况的编写程序及运行结果分别见附录8和附录9）,得到两种情况总路程分别为525.0932和527.2727米，然后用总路程减去相应的最小生成树屮已建好的道路和湖边的路，从而得到公园内部总的道路长度和最小，即两种情况的最优解分别为375.0932和377.2727米。第四种方案：piP2P3P4P5P6P7P8ABR1Xi205016020012035100310/113490/39140yj0005010010010025600/112200/3970点的坐标数据表九R214045R316545R416570闪部有六个交点，即找到确定的点A、B和湖面上的Rl、R2、R3、R4,己知14个点的坐标（见表九）。构造各边的权值为dij=Xj—X，|+1），y—）’，，（/矣y，/，J-=1，2,...，14）其屮U/，"为第/个点的坐标。然后以/^｛门，/?2，...么｝作为顶点集，构造赋权图6=（/£，140，这里VV=（wy）j4xi4为邻接矩|浑，其中％=如，/，J=1，2，...14。求公0道路的总路程最短的问题实际上就是求图G的最小生成树问题。 利用Matlab7.9版程序求解（编写程序及运行结果见附录10），得到总路程 为550.0932米，然后用总路程减去最小生成树中己建好的道路和湖边的路，从而得到公园内部总的道路长度和最小，即最优解为375.0932米。57.通过比较以上四种方案，得知第一种方案为最优方案。其最小生成树见下图，公园内部总的道路长度和最小，即最优解为275米。Node2Node8Node6Node3Node4Node10Node9Node7Node11727257750x4025Node1Node5六、误差分析对于题目中给出的数据，采用了Matlab程序求解，而求解的结果是存在一定的误差的，如在求解任意两点间的距离时，给出的结果都是整数解(见附录)但这些误差对于模型的建立没有影响。七、模型推广对本题进一步讨论：本问题设计的是一个长为200米，宽为100米的矩形公园，通过建立模型，给出了三问的最优解。(1)如果将此矩形扩大为原来的1倍，2倍，…，n倍，上面建立的三个最 优模型是否也成立呢？通过分析验证三个最优模型是成立的。注：验证方法为数学分析法，得知其对应的坐标点分别变为原来的21倍，22倍，...，2"倍，同样是编写Matlab程序(7.9版)找到最优解。(1)如果设计的是一个不规则形状的公园，其它条件不变，我们乂如何来确定内部路的交叉点，使总的道路长度和最小？八、模型的应用本模型可用于实际生活中的公园道路设计。九、模型评价1、模型的优点：(1)、本模型利用Matlab程序先找到完全图的最小生成树，看找到的最小生成树是否符合题屮的约束条件，符合即找到最优解。这样使得求解的过程简单易懂，且较直观，同时节约了如何来写约束条件的时间。(2)、本模型能与实际紧密联系，贴近实际，通用性较强。(3)、对于题中的一些问题都是应用计算机进行求解，若数据发生变动，可以很快得到结果，有较强的应用性。(4)、模型推广后，易于用于实际的公园设计问题，具有一定的普适性和实用性。2、模型的缺点：找点的方法及其编程较复杂。结合以上给点可以看出，本模型是一个较完善的模型。十、参考文献[1]司守奎，孙玺菁，《数学建模算法与应用》，北京：国防工业出版社，2011.8.[2]张磊，毕靖，郭莲英，《MATLAB使用教程》，北京：人民邮电出版社，2008.12[3]殷剑宏，吴开亚，《图论及其算法》，合肥：屮国科学技术大学出版社，2003.7.|4|周品，何正风，《MATLAB数值分析》，北京：机械工业出版社，2009.1.(5)王海英，黄强，《图论算法及其MATLAB实现》，北京：北京航空航天大学出版社，2010.2.[6]赫孝良，戴永红，周义仓，《数学建模竞赛》，西安：西安交通大学出版社，2002.6.[7]韩中庚，《数学建模竞赛》，北京：科学出版社，2007.5.[8]薛毅，《数学建模基础》，北京：科学出版社，2011.十一、附录问题一：1、计算程序(Matlab7.9版)如下：x=[2050160200120351005040120115]; y=[000501001001002575404070】；xy=[x;y】；d=mandist(xy);%求xy的两两列向:W:间的绝对值距离d=tril(d);%截取matlab工具箱要求的下三角矩阵b=sparse(d)%转化为稀疏矩陈[ST/pred]=graphminspantree(b,"Method"/,Kruskal1)%调用最小生成树的命令st=full(ST>;%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度view(biograph(ST,[]/ShowArrows7off","ShowWeights7on"))%画出最小生成树运行结果： 3014023020011511045105601401651102001701151407575501101359014022525018518516080115130215240225175170901058511019595140(2,1)(34)(4.1)(5.1)(6.1)(7,D(8,1)(9.1)(10,1)(114)(12,1)(3,2>(4.2)(5.2)(6.2)(7.2)(8.2)(9.2)(10,2)(11,2)(12,2)(4.3)(5.3)(6.3)(7.3)(8.3)(9.3)(10.3)(11.3)(12.3)(5.4)(6.4)(7.4)(8.4)(9.4)⑽4)(11.4)(12.4)(6.5)(7.5)(8.5)(9.5)(10.5) (11,5)60(12,5)35(7,6)25(8,6)110(9,6)40(10,6)65(11,6)145(12,6)110(87)85(9,7)65(10,7)90(117)170(12,7)135(9,8)100(10,8)55(11,8)135(12,8)160(10,9)45(11,9)105(12,9)70(11,10)80(12,10)105(12,11)35=(2,1)30(8,1)45(10,2)50(4,3)90(11,3)80(12,5)35(7,6)25(9,6)40(10,9)45(12,9)70(12,11)351102129pred=0111312TreeLength=545 Node12Node10£04535Node2Node8Node7|Node9Node4Node5Node1140.Node1|Node6Node3问题二：2、点A、B、C的交点坐标：(1)A的交点程序：symsxlylx2y2x3y3x4y4symsABCsymsxy%%计算Al,Bl，A2，B2xl=10;x2=50;x3=35;x4=20;yl=100;y2=0;y3=100;y4=0;eql=A*xl+B*yl+C;eq2=A*x2+B*y2+C;sovl=solve(eql,eq2,A,B);eq3=A*x3+B*y3+C;eq4=A*x4+B*y4+C;sov2=solve(eq3,eq4,A,B);Al=simplify(sovl.A/C);Bl=simplify(sovl.B/C);A2=simplify(sov2.A/C);B2=simplify(sov2.B/C);%Al=(yl-y2)/(xl*y2-x2*yl);%Bl=(-xl+x2)/(xl*y2-x2*yl);%%求交点eql=Al*x+Bl*y+l; A2=(y3-y4)/(x3*y4-x4*y3);B2=(-x3+x4)/(x3*y4-x4*y3);eq2=A2*x+B2*y+l;sov=solve(eql,eq2/x,y);pretty(sov.x)pretty(sov.y)运行结果：31011600(2)B的交点程序：symsxlylx2y2x3y3x4y4symsABCsymsxy%%计算Al,Bl，A2，B2xl=35;x2=160;x3=120;x4=50;yl=100;y2=0;y3=100;y4=0;eql=A*xl+B*yl+C;eq2=A*x2+B*y2+C;sovl=solve(eql,eq2,A,B);eq3=A*x3+B*y3+C;eq4=A*x4+B*y4+C;sov2=solve(eq3,eq4,A,B);Al=simplify(sovl.A/C);Bl=simplify(sovl.B/C);A2=simplify(sov2.A/C);B2=simplify(sov2.B/C);%Al=(yl-y2)/(xl*y2-x2*yl);%Bl=(-xl+x2)/(xl*y2-x2*yl);%%求交点eql=Al*x+Bl*y+l;A2=(y3-y4)/(x3*y4-x4*y3);B2=(-x3+x4)/(x3*y4-x4*y3);eq2=A2*x+B2*y+l;sov=solve(eql,eq2,x,y);pretty(sov.x)pretty(sov.y)运行结果：3490 2200(3)C的交点程序：①先求两条直线方程程序.•xl=200;x2=160;x3=200;yl=100;y2=0;y3=50;kl=(y2-yl)/(x2-xl);k2=-(x2-xl)/(y2-yl);bl=yl-kl*xl;b2=y3-k2*x3;Yl=kl*Xl+blY2=k2*X2+b2运行的结果：Y1=(5*Xl)/2-400Y2=130-(2*X2)/5②求交点程序：a=[2,5;5z-2];b=[650;800];c=ab运行结果：c=182.758656.89663、第一部一个交点B的运行程序：x=[2050160200120351003490/39];y=[00050100100100252200/59];xy=[x;y];d=mandist(xy);%求xy的两两列向量间的绝对值距离d=tril(d);%截取matlab工具箱要求的卜*三角矩阵b=sparse(d)%转化为稀疏矩阵[STzpred]=graphminspantree(b/Method"z,Kruskal")%调用最小生成树的命令st=full(ST>;%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度view(biograph(ST/[]/"ShowArrows,/off7ShowWeights7on"))%画出最小生成树运行结果：b=(2,1)30.0000(34)140.0000(44)230.0000(5,1)200.0000(6,1)115.0000 (74)110.0000(8,1)45.0000(94)125.8974(3.2)(4.2)110.0000200.0000(5,2)170.0000(6,2)(7,2)115.0000140.0000(8,2)(9,2)75.000095.8974(4,3)90.0000(5.3)(6.3)140.0000225.0000(7,3)250.0000(8,3)185.0000(9,3)126.9231(M)130.0000(6,4)215.0000(M)240.0000(8,4)225.0000(9,4)116.9231(6,5)85.0000(7,5)110.0000(8.5)(9.5)195.000074.1026(7,6)25.0000(8,6)(9,6)110.000098.0769(8,7)85.0000(9,7)123.0769(9,8)120.8974ST=(2,1)30.0000(8,1)45.0000(3,2)110.0000(4,3)90.0000(6,5)85.0000(9,5)74.1026(7,6)25.0000(8,7)85.0000pred=012367815TreeLength:=544.1026Node4 4、第二种方案：内部两个交点A、C的运行程序：x=[205016020012035100310/11182.7586];y=[0005010010010025600/1156.8966];xy=[x;y];d=mandist(xy);%求xy的两两列向量间的绝对值距离d=tril(d);%截取matlabK具箱要求的下三角矩阵b=sparse(d)%转化为稀疏矩阵[ST/pred]=graphminspantree(bz,Method,z"Kruskar)%调用最小生成树的命令st=full(ST>;%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度viewfbiographfSTJl/ShowArrows"/off"/ShowWeights"/on"))%画出最小生成树运行结果：b=(2.1)30.0000(3.1)140.0000(4.1)230.0000(5.1)200.0000(6.1)115.0000(7.1)110.0000(8.1)45.0000(9.1)62.7273(10,1)219.6552(3.2)110.0000 (4.2)(5.2)(6.2)(7.2)(8.2)(9.2)(10,2)(4.3)(5.3)(6.3)(7.3)(8.3)(9.3)(10.3)(5.4)(6.4)(M)(8.4)(94)(10.4)(6.5)(7.5)(8.5)(9.5)(10.5)(A6)(8.6)(9.6)(10.6)(8.7)(9.7)(10,7)(9.8)⑽8)(10,9)ST=(2,1)(8,1)(10.3)(10.4)(6.5)(10.5)(7.6)(9.6)200.0000170.0000115.0000140.000075.000076.3636189.655290.0000140.0000225.0000250.0000185.0000186.363679.6552130.0000215.0000240.0000225.0000176.363624.138085.0000110.0000195.0000137.2727105.862025.0000110.000052.2727190.862085.000063.6364215.862057.7273214.6552156.927930.000045.000079.655224.138085.0000105.862025.000052.2727 (9,8)57.7273pred=011010696TreeLength=504.65525、第三种方案：内部有3个交点A、B、C的运行程序x=[205016020012035100310/113490/59182.7586];y=[0005010010010025600/112200/3956.8966];xy=[x;y];d=mandist(xy);%求xy的两两列向量间的绝对值距离d=tril(d);%截取matlab工具箱要求的下三危矩陈b=sparse(d)%转化为稀疏矩陈[ST,pred]=graphminspantree(b,,Method,/,Kruskal")%调用最小生成树的命令st=full(ST>;%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度view(biograph(ST/[]/"ShowArrows,/off7ShowWeights7on"))%画出最小生成树运行结果：b=(2,1)30.0000(34)140.0000(4,1)230.0000(5,1)200.0000(6,1)115.0000(7,1)110.0000(8,1)45.0000 (94)62.7273(10,1)125.8974(11,1)219.6552(3,2)110.0000(4,2)200.0000(5,2)170.0000(6,2)115.0000(7,2)140.0000(8,2)75.0000(9,2)76.3636(10,2)95.8974(11,2)189.6552(4,3)90.0000(5,3)140.0000(6,3)225.0000(7,3)250.0000(8,3)185.0000(9,3)186.3636(10,3)126.9231(11,3)79.6552(5,4)130.0000(6,4)215.0000(M)240.0000(M)225.0000(9,4)176.3636(10,4)116.9231(11,4)24.1380(6,5)85.0000(7,5)110.0000(8,5)195.0000(9,5)137.2727(10,5)74.1026(11,5)105.8620(7,6)25.0000(8,6)110.0000(9,6)52.2727(10,6)98.0769(11,6)190.8620(8,7)85.0000(9,7)63.6364(10,7)123.0769(IV)215.8620(9,8)57.7273(10,8)120.8974 10TreeLength=544.8237(10.9)(11.9)(11.10)ST=(2,1)(8,1)(11.3)(11.4)(10.5)(7.6)(9.6)(9,8)(10,9)(11,10)pred=0111214.655263.1702156.927993.757830.000045.000079.655224.138074.102625.000052.272757.727363.170293.757811109问题三：6、第一种方案：内部有三个交点为A、R2、R3运行程序：x=[205016020012035100310/11140165】;y=[0005010010010025600/114545】；xy=[x;y]; d=mandist(xy);%求xy的两两列MU!:间的绝对值距离d=thl(d);%截取matlab工具箱要求的下三角矩阵b=sparse(d)%转化为稀疏矩阵[ST#pred]=graphminspantree(b/Method7Kruskar)%调用最小生成树的命令st=full(ST);%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度viewJbiographfST^J/ShowArrows"/off"/ShowWeightsVon"))%画出最小生成树运行结果b=(2,1)(3.1)(4.1)(5.1)(6.1)(74)(8,1)(9.1)(10,1)(11,1)(3.2)(4.2)(5.2)(6.2)(7.2)(8.2)(9.2)(10,2)(11,2)(4.3)(5.3)(6.3)(7.3)(8.3)(9.3)(10.3)(11.3)(5.4)(6.4)(7.4)(8.4)(9z4)(10.4)(11.4)(6.5)30.0000140.0000230.0000200.0000115.0000110.000045.000062.7273165.0000190.0000110.0000200.0000170.0000115.0000140.000075.000076.3636135.0000160.000090.0000140.0000225.0000250.0000185.0000186.363665.000050.0000130.0000215.0000240.0000225.0000176.363665.000040.000085.0000 (7,5)110.0000(8,5)195.0000(9,5)137.2727(10.5)(11.5)75.0000100.0000(7,6)25.0000(8,6)(9,6)110.000052.2727(10,6)(11,6)160.0000185.0000(8,7)85.0000(97)(10J)63.6364185.0000(117)210.0000(9,8)57.7273(10,8)160.0000(11,8)185.0000(10,9)121.3636(11,9)146.3636（n,io）25.0000ST=(2,1)30.0000(8,1)45.0000(11.3)(11.4)50.000040.0000(6,5)85.0000(10,5)(7,6)75.000025.0000(9,6)52.2727(9,8)57.7273(1140)25.0000pred=01111169618510TreeLength:=485 Node9Node1Node1157.舍§727254025xNode2Node8Node6Node3Node4Node10|Node1|Node57、第二种方案：内部有四个点A、B、R2、R3的运行程序：x=[205016020012035100310/113490/39140165];y=[0005010010010025600/112200/594545];xy=[x;y】；d=mandist(xy);%求xy的两两列向量间的绝对值距离d=thl(d);%截取matlab工具箱要求的下三角矩阵b=sparse(d)%转化为稀疏矩阵[ST/pred]=graphminspantree(b/Method"z"Kruskar)%调用最小生成树的命令st=full(ST>;%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度viewfbiographfSTJJ/ShowArrows"/off"/ShowWeights"/on"))%画出最小生成树运行结果：b=(2.1)30.0000(3.1)140.0000(4.1)230.0000(5.1)200.0000(6.1)115.0000(7.1)110.0000(8.1)45.0000(9.1)62.7273(10.1)125.8974(11.1)165.0000 (12,1)(3.2)(4.2)(5.2)(6.2)(A2)(8,2)(9.2)(10,2)(11,2)(12,2)(4.3)(5.3)(6.3)(A3)(8.3)(9.3)(10.3)(11.3)(12.3)(5.4)(M)(M)(8.4)(9.4)(10.4)(11.4)(12.4)(6.5)(7.5)(8.5)(9.5)(10.5)(11.5)(12.5)(7.6)(8.6)(9.6)(10.6)(11,6)(12,6)(8.7)(97)(10J)190.0000110.0000200.0000170.0000115.0000140.000075.000076.363695.8974135.0000160.000090.0000140.0000225.0000250.0000185.0000186.3636126.923165.000050.0000130.0000215.0000240.0000225.0000176.3636116.923165.000040.000085.0000110.0000195.0000137.272774.102675.0000100.000025.0000110.000052.272798.0769160.0000185.000085.000063.6364123.0769 (IV)(12,7)185.0000210.0000(9,8)(10,8)57.7273120.8974(11,8)160.0000(12,8)185.0000(10,9)63.1702(11,9)121.3636(12,9)146.3636(11,10)61.9231(12,10)86.9231(12,11)25.0000ST=(2,1)30.0000(8,1)45.0000(12.3)(12.4)50.000040.0000(10,5)(7,6)74.102625.0000(9,6)52.2727(9,8)57.7273(10,9)63.1702(11,10)(UH)61.923125.0000pred=01121210961891011TreeLength==524.1958 Node128、第三种方案的第一种情况：内部点为A、B、R2、Rl、R3的程序：x=[205016020012035100310/113490/39140140165];y=[0005010010010025600/112200/39457045];xy=[x;y];d=mandist(xy);%求*/的两两列向量间的绝对值距离d=thl(d>;%截収matlab工具箱要求的下三角矩阵b=sparse(d)%转化为稀疏矩陈[ST/pred]=graphminspantree(b/,Method,/"Kruskal,)%调用最小生成树的命令st=full(ST>;%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度viewfbiographfSTJl/ShowArrows"/off"/ShowWeights"/on"))%画出最小生成树运行结果：b=(2,1)30.0000(34)140.0000(4,1)230.0000(54)200.0000(6,1)115.0000(74)110.0000(8,1)45.0000(94)62.7273(10,1)125.8974(114)165.0000(12,1)190.0000 (13.1)(3.2)(4.2)(5.2)(6.2)(A2)(8,2)(9.2)(10.2)(11,2)(12,2)(13.2)(4.3)(5.3)(6.3)(7.3)(8.3)(9.3)(10.3)(11.3)(12.3)(13.3)(5.4)(6.3)(M)(8.4)(9.4)(10.4)(11.4)(12.4)(13.4)(6.5)(7.5)(8.5)(9.5)(10.5)(11.5)(12.5)(13.5)(A6)(8.6)(9,6)(10.3)(11,6)190.0000110.0000200.0000170.0000115.0000140.000075.000076.363695.8974135.0000160.0000160.000090.0000140.0000225.0000250.0000185.0000186.3636126.923165.000090.000050.0000130.0000215.0000240.0000225.0000176.3636116.923165.000080.000040.000085.0000110.0000195.0000137.272774.102675.000050.0000100.000025.0000110.000052.272798.0769160.0000 (12,6)135.0000(13,6)185.0000(8,7)85.0000(9,7)(107)63.6364123.0769(11,7)185.0000(12.7)(13.7)160.0000210.0000(9,8)(10,8)57.7273120.8974(11,8)160.0000(12,8)(13,8)185.0000185.0000(10,9)63.1702(11,9)121.3636(12,9)127.2727(13,9)146.3636(11,10)61.9231(12,10)64.1026(13,10)86.9231(12,U)25.0000(13,11)25.0000(1342)50.0000ST=(24)30.0000(8,1)45.0000(13.3)(13.4)50.000040.0000(12,5)50.0000(7,6)25.0000(9,6)52.2727(9,8)(10,9)57.727363.1702(11,10)61.9231(12,11)25.0000(13,U)25.0000pred=0113131296189101111TreeLength=525.0932 Node1|9、第三种方案的第二种情况内部的点为：A、B、Rl、R4、R3运行程序：x=[205016020012035100310/113490/59140165165];y=[0005010010010025600/112200/39707045];xy=[x;y】；d=mandist(xy);%求xy的两两列向量间的绝对值距离d=tril(d);%截取matlabT具箱要求的下三角矩阵b=sparse(d)%转化为稀疏矩阵[ST/pred]=graphminspantree(b/Method"z"Kruskar)%调用最小生成树的命令st=full(ST);%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度viewfbiographfSTJJ/ShowArrows"/off"/ShowWeights"/on"))%画出最小生成树运行的结果：b=(2,1)30.0000(3,1)140.0000(4,1)230.0000(54)200.0000(6,1)115.0000(AD110.0000(8,1)45.0000(94)62.7273(10,1)125.8974(11,1)190.0000 (12,1)(13.1)(3.2)(4.2)(5.2)(6.2)(7.2)(8.2)(9.2)(10.2)(IV)(12,2)(13.2)(4.3)(5.3)(6.3)(7.3)(8.3)(9.3)(10.3)(11.3)(12.3)(13.3)(5.4)(6.4)(M)(8.4)(9.4)(10.4)(11.4)(12.4)(13.4)(6.5)(A5)(8.5)(9.5)(10.5)(11.5)(12.5)(13.5)(7.6)(8.6)(9,6)(10.6)215.0000190.0000110.0000200.0000170.0000115.0000140.000075.000076.363695.8974160.0000185.0000160.000090.0000140.0000225.0000250.0000185.0000186.3636126.923190.000075.000050.0000130.0000215.0000240.0000225.0000176.3636116.923180.000055.000040.000085.0000110.0000195.0000137.272774.102650.000075.0000100.000025.0000110.000052.272798.0769 (11,6)135.0000(12,6)160.0000(13,6)185.0000(8,7)(V)85.000063.6364(107)123.0769(11.7)(12.7)160.0000185.0000(IV)(9,8)210.000057.7273(10,8)120.8974(11,8)(U8)185.0000210.0000(13,8)185.0000(10,9)63.1702(11,9)127.2727(12,9)152.2727(13,9)146.3636(11,10)64.1026(12,10)89.1026(13,10)86.9231(12,11)25.0000(1341)50.0000(13,12)25.0000ST=(2,1)30.0000(8,1)(13,3)45.000050.0000(13,4)40.0000(11,5)50.0000(7,6)25.0000(9,6)(9,8)52.272757.7273(10,9)63.1702(1140)64.1026(12,U)25.0000(13,12)25.0000pred=0113131196189101112TreeLength=527.2727Node13Node3|Node4Node12,50z^02525 Node11Node5Node1063.1702Node7|Node950/p4.1026Node2Node6|Node8Q0z-45Node110、第四种方案内部的点为：A、B、Rl、R2、R3、R4运行程序：x=[205016020012035100310/113490/39140140165165];y=[0005010010010025600/112200/3970454570];xy=[x;y];d=mandist(xy);%求xy的两两列向量间的绝对值距离d=tril(d);%截取matlab工具箱要求的下三角矩阵b=sparse(d)%转化为稀疏矩陈[ST,pred]=graphminspantree(b,,Method,z,Kruskal")%调用最小生成树的命令st=full(ST);%把最小生成树的稀疏矩阵转化成普通矩阵TreeLength=sum(sum(st))%求最小生成树的长度viewfbiographfSTJl/ShowArrows"/off"/ShowWeights"/on"))%画出最小生成树运行结果：b=(2.1)30.0000(3.1)140.0000(4.1)230.0000(5.1)200.0000(6.1)115.0000(7.1)110.0000(8.1)45.0000(9.1)62.7273 (10,1)(11,1)(12,1)(13.1)(Hl)(3.2)(4.2)(5.2)(6.2)(7.2)(8.2)(9.2)(10.2)(11,2)(12,2)(13.2)(14.2)(4.3)(5.3)(6.3)(A3)(8.3)(9.3)(10.3)(11.3)(12.3)(13.3)(14.3)(5.4)(6.4)(M)(8.4)(9.4)(10.4)(11.4)(12.4)(13.4)(14.4)(6.5)(A5>(8.5)(9.5)(10.5)(11.5)125.8974190.0000165.0000190.0000215.0000110.0000200.0000170.0000115.0000140.000075.000076.363695.8974160.0000135.0000160.0000185.000090.0000140.0000225.0000250.0000185.0000186.3636126.923190.000065.000050.000075.0000130.0000215.0000240.0000225.0000176.3636116.923180.000065.000040.000055.000085.0000110.0000195.0000137.272774.102650.0000 (12.5)(13.5)(14.5)(7.6)(8.6)(9.6)(10.6)(11,6)(12,6)(13.6)(H6)(8.7)(97)(10.7)(IV)(12.7)(13.7)(147)(9.8)(10.8)(11,8)(12,8)(13.8)(14?8)(10.9)(11.9)(12.9)(13.9)(14.9)(11.10)(1240)(13.10)(14.10)(12.11)(13.9)(HU)(13.12)(14.12)(14.13)ST=(2,1)(8,1)(13.3)(13.4)75.0000100.000075.000025.0000110.000052.272798.0769135.0000160.0000185.0000160.000085.000063.6364123.0769160.0000185.0000210.0000185.000057.7273120.8974185.0000160.0000185.0000210.000063.1702127.2727121.3636146.3636152.272764.102661.923186.923189.102625.000050.000025.000025.000050.000025.000030.000045.000050.000040.0000 (11,5)50.0000(7,6)25.0000(9,6)52.2727(9,8)57.7273(10,9)63.1702(12,10)61.9231(12,11)25.0000(14,11)25.0000(13,12)25.0000pred=Columns1through131201131311961891210Column1411TreeLength=550.0932Node1