CASIO编程在路线设计中的应用A 14页

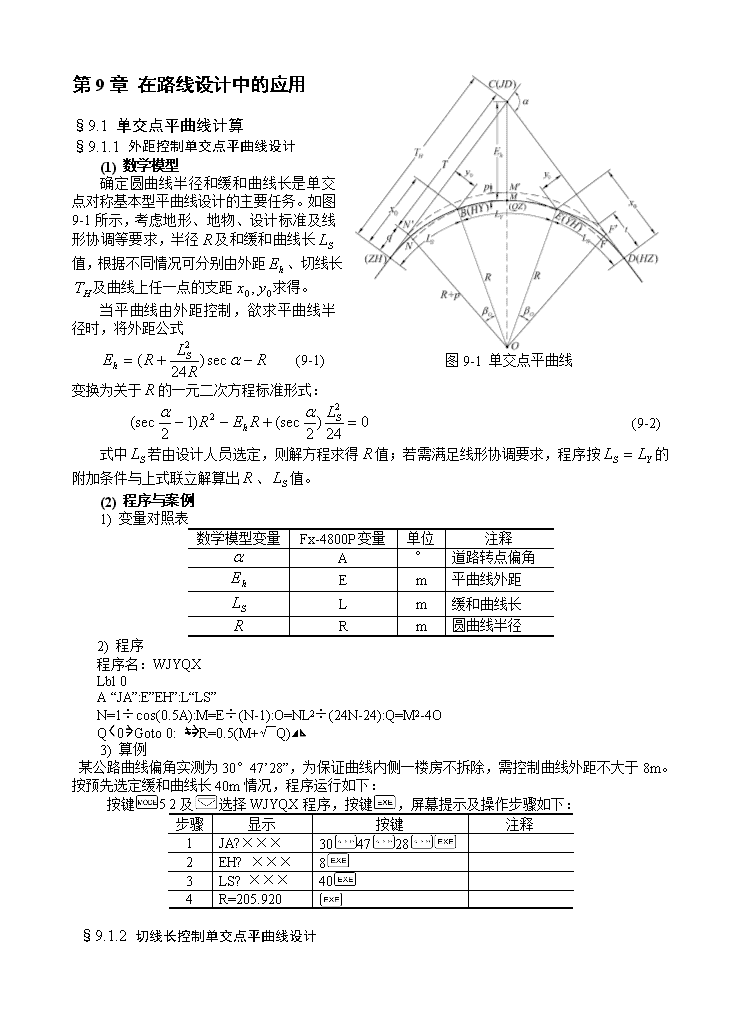
图9-1单交点平曲线第9章在路线设计中的应用§9.1单交点平曲线计算§9.1.1外距控制单交点平曲线设计(1)数学模型确定圆曲线半径和缓和曲线长是单交点对称基本型平曲线设计的主要任务。如图9-1所示，考虑地形、地物、设计标准及线形协调等要求，半径及和缓和曲线长值，根据不同情况可分别由外距、切线长及曲线上任一点的支距求得。当平曲线由外距控制，欲求平曲线半径时，将外距公式(9-1)变换为关于的一元二次方程标准形式：(9-2)式中若由设计人员选定，则解方程求得值；若需满足线形协调要求，程序按的附加条件与上式联立解算出、值。(2)程序与案例1)变量对照表数学模型变量Fx-4800P变量单位注释A°道路转点偏角Em平曲线外距Lm缓和曲线长Rm圆曲线半径2)程序程序名：WJYQXLbl0A“JA”:E”EH”:L“LS”N=1÷cos(0.5A):M=E÷(N-1):O=NL2÷(24N-24):Q=M2-4OQ0Goto0:R=0.5(M+Q)3)算例某公路曲线偏角实测为30°47’28”，为保证曲线内侧一楼房不拆除，需控制曲线外距不大于8m。按预先选定缓和曲线长40m情况，程序运行如下：按键52及选择WJYQX程序，按键，屏幕提示及操作步骤如下：步骤显示按键注释1JA?×××3047282EH?×××83LS?×××404R=205.920§9.1.2切线长控制单交点平曲线设计 (1)数学模型各项条件同§9.1.1，当切线长固定，欲求平曲线半径时，将切线长公式(9-3)变换为关于的一元三次方程：(9-4)可使用牛顿法编程求解。(2)程序与案例1)变量对照表数学模型变量f-4800P变量单位注释A°道路转点偏角Tm平曲线外距Lm缓和曲线长Jm迭代计算的精度Rm圆曲线半径2)程序程序名：QXYQXA“JA”:T“TH”:L“LS”:J“JINDU”N=tan(A÷2):M=L2N÷24:O=-L^3÷240:Q=0.5L-T:S=-Q÷MLbl1U=NS^3+QS2+MS+O:V=3NS2+2QS+M:R=S-U÷VAbs(R-S)JS=R:Goto1:R”R=“3)算例某公路曲线偏角实测为30°47′8″，为保证曲线内侧一楼房不拆除，需控制曲线外距不大于8m，预先选定缓和曲线长40m情况，程序运行如下：按键52及选择QXYQX程序，按键，屏幕提示及操作步骤如下：步骤显示按键1JA?×××2630272TH?×××97.793LS?×××404JINDU?×××0.0015R=308.680§9.1.3设置不对称缓和曲线单交点平曲线计算(1)数学模型如图9-2所示，单交点平曲线交点为JD，转角为，设计圆曲线半径为，第一缓和曲线长度为，第二缓和曲线长度为，求平曲线要素及主点桩号。公式如下：切线1增量：(9-5)切线2增量：(9-6) 曲线内移值1：(9-7)图9-2设置不对称缓和曲线的基本平曲线曲线内移值2：(9-8)切线1长：(9-9)切线2长：(9-10)第一缓和曲线角：(9-11)第二缓和曲线角：(9-12)圆曲线长：(9-13)曲线长：(9-14)主点桩号：第一缓和曲线起点：第一缓和曲线终点(即圆曲线起点)：圆曲线中点：第二缓和曲线起点(即圆曲线终点)：第二缓和曲线终点：(2)程序与案例1)变量对照表数学模型变量fx-4800P变量单位注释K°′″路线转角 Rm圆曲线半径Jm交点桩号Nm第一缓和曲线长度Mm第二缓和曲线长度Qm切线1增量Sm切线2增量Pm曲线内移值1Um曲线内移值2B°′″第一缓和曲线角V°′″第二缓和曲线角Tm曲线切线1长Wm曲线切线2长Ym圆曲线长Lm曲线全长Am第一缓和曲线起点Cm第一缓和曲线终点Dm圆曲线终点Fm第二缓和曲线起点Gm第二缓和曲线终点2)程序程序名：NCJSTAKEK”JA”:R:”R”:J”JDZH”:N”LS1”:M”LS2”Q=N÷2-N^3÷240R2S=M÷2-M^3÷240R2P=N2÷24R-N^4÷2384R^3U=M2÷24R-M^4÷2384R^3B=28.6479N÷RV=28.6479M÷RT=(R+U)tan(K÷2)+Q+(P-U)÷tanKW=(R+U)tan(K÷2)+S+(P-U)÷sinKY=0.0174533R(K–B-V)L=Y+N+MA”ZH”=J-TC”HY”=A+ND”QZ”=C+0.5YF”YH”=D+0.5YG”HZ”=F+M3)操作步骤设路线某转点JD的资料如表9-1所示，求平曲线要素及曲线主点桩号。表9-1计算案例JA28°30′R(m)400JDAZH(m)15468.280Ls1(m)700Ls2(m)100按键52及选择NCJSTAKE程序，按键，屏幕提示及操作步骤如下： 步骤显示按键注释1JA?×××2830路线转角2R?×××400圆曲线半径3JDZH?×××15468.280交点桩号4LS1?×××70第一缓和曲线长度5LS2?×××100第二缓和曲线长度6Q=34.991切线1增量7S=49.974切线2增量8P=0.510曲线内移值19U=1.042曲线内移值110B=5.01338°第一缓和曲线角11V=7.1620°第二缓和曲线角12T=135.863曲线切线1长13W=159.611曲线切线2长14Y=113.967圆曲线长15L=283.967曲线全长16ZH=15332.417第一缓和曲线起点17HY=15402.417第一缓和曲线终点18QZ=15459.400圆曲线终点19YH=15516.384第二缓和曲线起点20HZ=15616.384第二缓和曲线终点§9.1.4单交点双圆曲线计算(1)数学模型如图9-3所示，单交点圆曲线交点为JD，转角为，设计圆曲线半径为，求平曲线要素及主点桩号。公式如下：切线1长(9-15)切线2长：(9-16)图9-3单交点双圆曲线曲线1长(9-17)曲线2长(9-18)曲线长(9-19)主点桩号：圆曲线起点：圆曲线公切点：圆曲线终点：(2)程序与案例1)变量对照表数学模型变量fx-4800P变量单位注释K°′″圆心角1M°′″圆心角2 Rm圆曲线半径1Sm圆曲线半径2Jm交点桩号Tm圆曲线切线长1Wm圆曲线切线长2Lm圆曲线曲线长Am圆曲线起点Bm圆曲线公切点Cm圆曲线终点2)程序程序名：SJDYSTAKEK”JA1”:M”JA2”:R:”R1”:S:”R2”:J”JDZH”D=Rtan(0.5K):E=Stan(0.5M)T”T1”=D+(D+E)sinM÷sin(K+M)W”T2”=E+(D+E)sinK÷sin(K+M)U=3.1416RK÷180:V=3.1416RM÷180L=U+VA”ZY”=J-TB”GQ”=A+UC”YZ”=B+V3)操作步骤设路线某转点JD的资料如表9-2所示，求平曲线要素及曲线主点桩号。表9-2计算案例JA118°30′R1(m)250JDAZH(m)1562.354JA220°12′R2(m)200按键52及选择SJDYSTAKE程序，按键，屏幕提示及操作步骤如下：步骤显示按键1JA1?×××18302JA2?×××20123R1?×××2504R2?×××2005T1=87.8756T2=74.3677L=151.2338ZY=1474.4799GQ=1555.20010YZ=1625.712§9.2多交点平曲线设计§9.2.1不与基线相切双交点单圆曲线计算(1)数学模型在选线时，由于地形和地物的限制，导线交点不能布置在理想的位置，在这种情况下，路线导线往往采取虚交的方式，如图9-4所示。A和B是路线导线的两个交点，AB为辅助导线，也称基线，为两交点的转角，为虚交点，分别是曲线起点和终点至的切线长。在△ABC中有，由正弦定理 ，(9-20)同理：(9-21)故有：(9-22)式中，，曲线长。(2)程序与案例1)变量对照表数学模型变量fx-4800P变量单位注释Rm圆曲线半径Km基线长度C°′″A点转角D°′″B点转角Jm交点桩号E°′″路线转角Tm切线长Qm切线1长Sm切线2长Lm圆曲线长Um圆曲线起点Vm圆曲线中点Ym圆曲线终点2)程序图9-4不与基线相切双交点单圆曲线程序名：XJDYQXLbl0R:K”AB”:C”A1”:D”A2”:J”JDA”E”ZHUANJ”=C+DA=KsinC÷sinE:B=KsinD÷sinET=Rtan(0.5E)Q”T1”=T-BS”T2”=T-AL=0.0174533REU”ZY”=J-QV”QZ”=U+0.5LY”YZ”=U+L3)操作步骤表9-3计算案例数据(m)10055°56′(m)58.13012°02′(m)2536.120按键52及选择XJDYQX程序，按键，屏幕提示及操作步骤如下：步骤显示按键注释 1R?×××输入圆曲线半径2AB?×××100输入基线长度3A1?×××58.13输入A点转角4A2?×××5556输入B点转角5JDA?×××1202输入A点桩号6ZHUANJ=67.9672536.120路线转角767°58′8T=67.408切线长9T1=54.334切线1长10T2=15.460切线2长11L=118.624圆曲线长12ZY=2481.786圆曲线起点13QZ=2541.098圆曲线中点14YZ=2600.410圆曲线终点图9-5与基线相切双交点圆曲线§9.2.2与基线相切双交点单圆曲线计算(1)数学模型如图9-5所示，为控制曲线的平面位置，要求圆曲线与基线相切，在这种情况下，圆曲线半径R由下式确定：(9-23)求出后，由下列公式求出，(9-24)(9-25)(2)程序与案例1)变量对照表数学模型变量fx-4800P变量单位注释Km基线长度C°′″A点转角D°′″B点转角Jm交点A桩号E°′″路线转角Rm圆曲线半径Tm切线长Qm切线1长Sm切线2长Lm圆曲线长Um圆曲线起点Vm圆曲线中点Ym圆曲线终点 2)程序程序名：JQ2JYQXLbl0K”AB”:C”A1”:D”A2”:J”JDA”E”ZHUANJ”=C+DR=K÷(tan(0.5C)+tan(0.5D)):T=Rtan(0.5E)Q”T1”=Rtan(0.5C)S”T2”=Rtan(0.5D)L=0.0174533REU”ZY”=J-QV”QZ”=U+0.5LY”YZ”=U+L3)操作步骤表9-4计算案例数据32°28′AB(m)73.25825°17′JDA(m)15782.631按键52及选择JQ2JYQX程序，按键，屏幕提示及操作步骤如下：步骤显示按键注释1AB?×××输入基线长度2A1?×××73.258输入A点转角3A2?×××3228输入B点转角4JDA?×××2517输入A点桩号5ZHUANJ=57.7515782.631路线转角657°45′7R=142.125圆曲线半径8T=78.376切线长9T1=41.381切线1长10T2=31.877切线2长11L=143.252圆曲线长12ZY=1574.250圆曲线起点13QZ=15812.876圆曲线中点14YZ=15884.502圆曲线终点图9-6与基线转向相反双交点单圆曲线§9.2.3基线转向相反双交点单圆曲线计算(1)数学模型如图9-6所示，由于地形的障碍，使得A、B两交点的转角、转向相反，在这种情况下，，因此有：(9-26)(9-27)(9-28)(2)、程序与案例1)变量对照表 数学模型变量fx-4800P变量单位注释Rm圆曲线半径Km基线长度C°′″A点转角D°′″B点转角Jm交点桩号E°′″路线转角Tm切线长Qm切线1长Sm切线2长Lm圆曲线长Um圆曲线起点Vm圆曲线中点Ym圆曲线终点2)程序程序名：JXFYQXLbl0R:K”AB”:C”A1”:D”A2”:J”JDA”E”ZHUANJ”=D-CA=KsinC÷sinE:B=KsinD÷sinET=Rtan(0.5E)Q”T1”=T-BS”T2”=T+AL=0.0174533REU”ZY”=J-QV”QZ”=U+0.5LY”YZ”=U+L3)操作步骤表9-5计算案例数据R(m)15055°17′AB(m)47.658118°02′JDA(m)25123.600按键52及选择JXFYQX程序，按键，屏幕提示及操作步骤如下：步骤显示按键注释1R?150输入圆曲线半径2AB?47.658输入基线长度3A1?5517输入A点转角4A2?11802输入B点转角5JDA?25123.600输入A点桩号6ZHUANJ=62.75路线转角762°45′8T=91.471切线长9T1=44.153切线1长10T2=135.535切线2长11L=164.279圆曲线长12ZY=25079.447圆曲线起点13QZ=25161.586圆曲线中点 14YZ=25243.726圆曲线终点§9.2.4三点虚交单圆曲线计算(1)数学模型图9-7三点虚交单圆曲线当地形比较复杂，两点虚交形式也不能解决问题时，可考虑采用三点虚交的导线，如图9-7所示，基线，，A、B、C点的转角分别为，延长AB和另一导线边FC的延长线相交于N点，在△NBC中，∠BND=，(9-29)(9-30)在△AND中，，(9-31)(9-32)(9-33)(2)、程序与案例1)变量对照表数学模型变量fx-4800P变量单位注释Rm圆曲线半径Km基线AB长度Nm基线BC长度C°′″A点转角D°′″B点转角F°′″C点转角Jm交点桩号E°′″路线转角TTm切线长T1Qm切线1长T2Sm切线2长LLm圆曲线长ZYUm圆曲线起点QZVm圆曲线中点YZYm圆曲线终点2)程序程序名：TRIJDYQXLbl0R:K”AB”:N”BC”:C”A1”:D”A2”:F”A3”:J”JDA”E”ZHUANJ”=C+D+FA=NsinF÷sin(D+F):B=NsinD÷sin(D+F):G=(K+A)sin(D+F)÷sinE H=(K+A)sinC÷sinE:T=Rtan(0.5E)Q”T1”=T-GS”T2”=T-H-BL=0.0174533REU”ZY”=J-QV”QZ”=U+0.5LY”YZ”=U+L3)操作步骤表9-6计算案例数据R(m)16035°15′JDA(m)3570.000AB(m)33.15026°23′BC(m)46.38017°15′按键52及选择TRIJDYQX程序，按键，屏幕提示及操作步骤如下：步骤显示按键注释1R?160输入圆曲线半径2AB?33.150输入基线AB长度3BC?46.380输入基线BC长度4A1?3515输入A点转角5A2?2623输入B点转角6A3?1715输入C点转角7JDA?3570.000输入A点桩号8ZHUANJ=78.883路线转角978°53′10T=131.620切线长11T1=94.291切线1长12T2=70.530切线2长13L=220.284圆曲线长14ZY=3475.709圆曲线起点15QZ=3585.851圆曲线中点16YZ=3695.993圆曲线终点图9-8多交点单圆曲线§9.2.5多点虚交单圆曲线计算(1)数学模型当地形很复杂，上述虚交形式也不能解决问题时，可考虑采用多点虚交的导线，如图9-8所示，在主导线CV和CW上设置辅助点A、B，用辅助导线D2D3…Dn将A、B连接起来，相应于A、D2、D3…Dn、B处的转角，符号当与一致时为正，相反为负，，，…，主导线转角为各辅助导线点的转角之代数和：(9-34)设A点的坐标为，则由第二章的相关程序计算出B点的坐标，以及AB的方位角，连同AC的方位角、BW的方位角一起，得到： (9-35)(9-36)(9-37)(9-38)(2)、程序与案例1)变量对照表数学模型变量fx-4800P变量单位注释Rm圆曲线半径Km基线AB长度C°′″AB方位角D°′″AC方位角Jm交点A桩号E°′″路线转角Tm切线长Qm切线1长Sm切线2长Lm圆曲线长Um圆曲线起点Vm圆曲线中点Ym圆曲线终点2)程序程序名：MJDYQXLbl0R:K”LAB”:C”AAB”:D”AAC”:E”ABW”:J”JDA”G=Abs(C-D):H=Abs(E-C):E”ZHUANJ”=G+HA=KsinG÷sinE:B=KsinH÷sinE:T=Rtan(0.5E)Q”T1”=T-BS”T2”=T-AL=0.0174533REU”ZY”=J-QV”QZ”=U+0.5LY”YZ”=U+L3)操作步骤表9-7计算案例数据R(m)200JDA(m)6587.32057°36′AB(m)75.55873°56′129°15′按键52及选择MJDYQX程序，按键，屏幕提示及操作步骤如下：步骤显示按键注释1R?200输入圆曲线半径2AB?75.558输入基线AB长度3A1?7356输入AB角4A1?5736输入AC角 5A2?12915输入BW点转角6JDA?6587.320输入A点桩号7ZHUANJ=71.65路线转角871°39′9T=144.377切线长10T1=78.916切线1长11T2=121.990切线2长12L=250.106圆曲线长13ZY=6508.404圆曲线起点14QZ=6633.456圆曲线中点15YZ=6758.510圆曲线终点