街道清扫路线设计--欧拉模型 21页

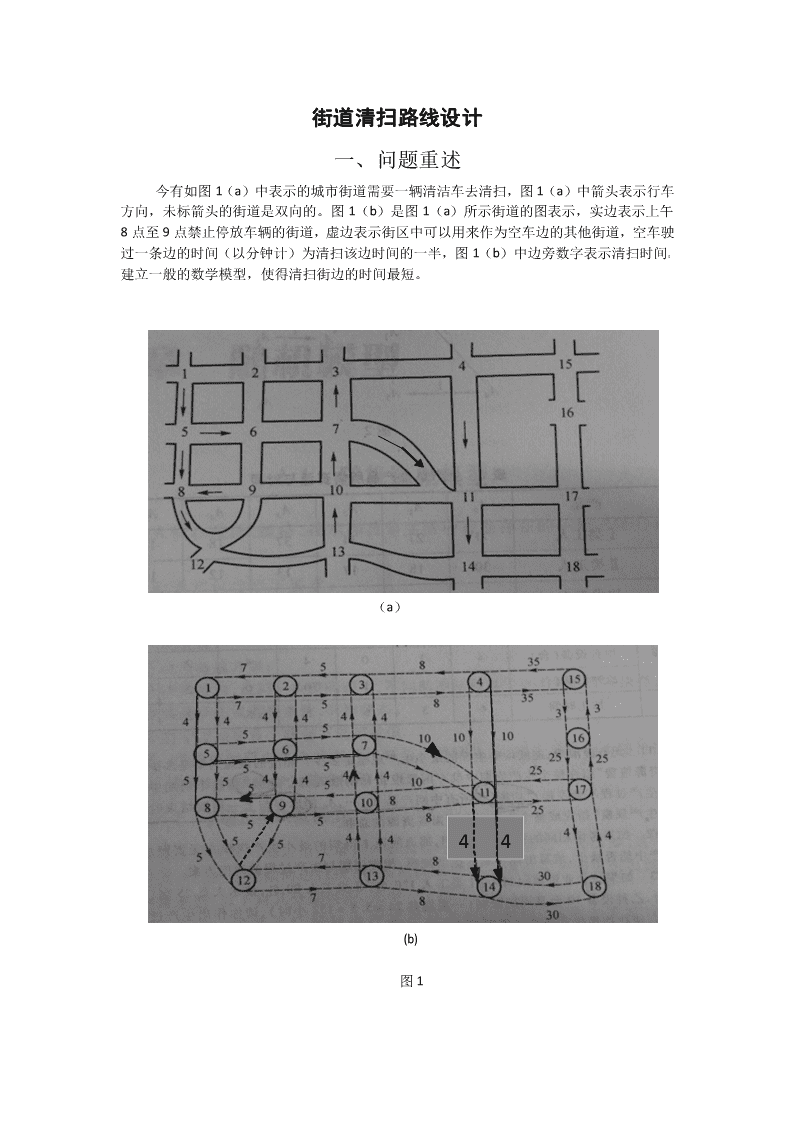
数学建模第二次作业清洁车模型生产调度模型数模第十四小组周永壮刘丽萍黄维 街道清扫路线设计一、问题重述今有如图1（a）中表示的城市街道需要一辆清洁车去清扫，图1（a）中箭头表示行车方向，未标箭头的街道是双向的。图1（b）是图1（a）所示街道的图表示，实边表示上午8点至9点禁止停放车辆的街道，虚边表示街区中可以用来作为空车边的其他街道，空车驶过一条边的时间（以分钟计）为清扫该边时间的一半，图1（b）中边旁数字表示清扫时间。建立一般的数学模型，使得清扫街边的时间最短。（a）44(b)图1 二、问题分析在本问题中，可将街区中的街道视为边，两条街道的交点视为顶点，构造表示街区的连通图。为了完成清扫街边的任务，清洁车必须驶过所有的街边，这便是图论中连通图的边遍历问题。为了完成图的遍历，对于Euler图而言，只需找出其中的Euler闭径即可；而对于实际问题而言，其图往往不是Euler图，例如本题的图，于是就要将一般的图转化为Euler图，在这个过程中不可避免的会添加一些辅助边，对于本题而言，这些辅助边就是清洁车重复走过的路程，也是它开空车的路程。三、模型假设1、单行道是比较窄的街道，只允许并排行驶一辆车，因此清洁车可以一次清扫整个街道。双向道是比较宽的街道，具有两个方向，清洁车严格遵守交通规则，不会在一条街道的两边之间来回穿梭。因此清洁车只能两次分别清扫街道的两边。根据题目要求，每条街道的两条边的清扫不一定是连在一起的。2、忽略清洁车的加油、维修、交通堵塞等意外情况耽误的时间，街道路面上的不清洁程度是均匀的，清洁车可以连续稳定地工作。3、整个街区设置有理想的垃圾倾倒点，即可以忽略清洁车倾倒垃圾的时间。4、街道交点不需要特别的清扫技术，即清洁车不会在这些地点耗费额外的时间。5、清洁车的起始点是任意的，根据实际情况，清洁车的起始清扫点应该是离清洁公司最近的街道点。根据朝九晚五的都市生活规律，规定起始时间点为9点。6、清洁车司机完全熟悉该街区的街道分布，不会盲目清扫。四、模型建立首先做出街区图如下图2，它是有向连通图。记为GVE(,)，其中V={1,2,⋯,18}。图2 预备定理连通的有向图存在Euler回路的充分必要条件是对任意节点，进入该节点边数（进数）与离开该节点边数（出数）相等。（证略）图2不满足预备定理的条件，故不存在Euler回路，因此需在原图中添加新边，构造出有向Euler图。对任意节点x，令dx()=出数-进数。若dx()<0，则称节点x为负节点；若dx()>0，则称节点x为正节点。显然，负节点存在过剩的进入边，正节点存在过剩的发出边，过剩的边数均为dx()。为了构造一个Euler图，必须添加一些新的边，设附加边集为E′，使GVE′(,+E′)中每个节点的dx()均为0即可。从而原来的街道清扫问题转化为怎样添加一些新的边E′，使图GVE′(,+E′)成为Euler图，且E′的权数为最小。由于任意有向边的两个节点，总有一个出发点和一个进入点，因此负节点和正节点总是成对出现的（当dx()=-2时，作为2个负节点）。而有效地添加新的有向边应该从负节点通向正节点。因此，构造Euler图问题转化为怎样把负节点与正节点组对，并使组对后的附加最短路的权数之和最小。具体实现如下：第一步，找出图2中的全部负、正节点，并把dx()标在节点旁。如下图3。图3负节点为：3，6，8，11，12，14；正节点为：1，4，5，7，9，13。每个正、负节点的dx()均为1。 第二步，求出每对正、负节点之间最短路的权数，并列于下表1中。表1节点1457913312816141325611171554168253129191012112824321213121220262414571432283616178注：最短路问题可采用Dijkstra算法或者Floyd算法。令矩阵⎡12816141325⎤⎢⎥1117155416⎢⎥⎢253129191012⎥D=(d)=⎢⎥ij⎢282432121312⎥⎢2026241457⎥⎢⎥⎣32283616178⎦则寻求最佳组对问题即是求解最优问题：6min∑dij,jjjjjji123456i=1其中，jjjjjj为1，2，3，的一个全排列。4123456编程计算可知：6min∑dijjjjjjji123456i=1=d+d+d+d+d+d⋯(1)122133445566=d+d+d+d+d+d⋯(2)122135445366=d+d+d+d+d+d⋯(3)122331445566=d+d+d+d+d+d⋯(4)122335445166=73注：程序见附件。 6从而可知，存在四种不同的dij取值方案使∑dij达到最小值73。ii=1当取方案（1）时，得到最佳组如下，用虚线表示相应的最短路，如图4（a）。3→4,6→1,8→5,11→7,12→9,14→13当取方案（2）时，得到最佳组对如下，用虚线表示相应的最短路，如图4（b）。3→4,6→1,8→9,11→7,12→5,14→13当取方案（3）时，得到最佳组对如下，用虚线表示相应的最短路，如图4（c）。3→4,6→5,8→1,11→7,12→9,14→13当取方案（4）时，得到最佳组对如下，用虚线表示相应的最短路，如图4（d）。3→4,6→5,8→9,11→7,12→1,14→13（a）（b） (c)(d)图4第三步，图4中的（a）（b）（c）（d）四个图都是Euler图，虚线表示附加边，它是开空车的路程。根据图论中的相关理论，Euler图中必存在包含所有弧的有向闭迹。于是，回到实际问题中来，清洁车从任意街道交点出发，必能沿着某一条路径扫完所有的街道，最终回到起始点。五、模型求解与结果分析在根据（1）（2）（3）（4）安排行车路径的情况下，设清洁车清扫街道的时间为T，开空车的时间分别为τ，τ，τ，τ。T即为图1（b）中所有时间之和。1234经过简单计算可知： T=436min，73τ=τ=τ=τ=min=36.5min≜τ12342于是，清洁车清扫街边的最短时间是：T=T+τ=436min36.5min+=472.5minmin再不考虑节点配对的情况下，图4中的（a）（b）（c）（d）四个图在图论的观点下是完全一样的。观察得到的欧拉图可知，若与一个节点所连的边数为2m，则该节点必在路线中出现m。又因为欧拉图可以看作是多个子图的叠加，于是包含该节点的子图必有m个。然而欧拉图的每一个子图又可以看作是一条独立的回路，于是可以通过以下方法寻找可行的路径：第一步：任意选取一个节点O作为起点和终点；第二步：任意选取一条可以从O点出发并最终回到O点的路径，称为“一级路径”；第三步：以一级路径上每一个节点为新的起点和终点寻找能够构成回路的“二级路径”（如有需要还可以寻找三级或者更高级的路径）；……如此下去直到所有的节点都满足：其所连边数的1/2等于它在各路线中出现的总次数。第四步：把所有的二级路径插入到一级路径中去（更一般地，把所有的k+1级路径插入到k级路径中），构成一个完整的回路。大致思路如图所示：二级路径三级路径一级路径 下面给出一种行车路线：1→5→8→12→13→14→18→17→16→15→4→3→2→1→2→6→7→11→17→11→10→11→14→13→10→9→12→9→6→2→3→4→15→16→17→18→14→13→12→9→8→12→9→10→7→3→4→11→10→7→6→2→1→5→6→9→6→2→1注：该路线并不唯一，而且起始点可以任意选择。六、进一步讨论模型优缺点：优点：1、目标街区已经被完全清扫；2、清扫路径很清晰，避免走太多的重复路径。缺点：1、为简化模型，忽略了一些实际情况；2、构造出的街区Euler图中存在不止一条行车路径，模型求解中并没有把所有路径都找出来。模型的改进方向：本模型中只考虑了一辆清洁车，最后计算出来的时间接近一个工作日，清扫街区的时间跨度过长，不利于城市整体面貌的展现，而考虑更多的清洁车同时进行清扫任务必然会缩短时间，提高工作效率，所以建立“具有多个清洁车辆的清扫路径问题”是具有实际意义的。这时，就需要根据图论理论，将图4中的街区Euler图分解成弧不交的回路的并。然后每一条回路的清扫任务由一辆清洁车承担，多辆清洁车同时工作。七、参考文献[1]谢政，戴丽.组合图论.长沙：国防科技大学出版社，2003.[2]陈东彦，李冬梅，王树忠.数学建模.北京：科学出版社，2007.八、附件61、计算min∑dij的代码：jjjjjji123456i=1#includeusingnamespacestd;intmain(){inta[6][6]={{12,8,16,14,13,25},{11,17,15,5,4,16},{25,31,29,19,10,12},{28,24,32,12,13,12},{20,26,24,14,5,7},{32,28,36,16,17,8}};for(inti=0;i<6;i++) for(intj=0;j<6;j++)for(intk=0;k<6;k++)for(intl=0;l<6;l++)for(intm=0;m<6;m++)for(intn=0;n<6;n++){if(i!=j&&i!=k&&i!=l&&i!=m&&i!=n&&j!=k&&j!=l&&j!=m&&j!=n&&k!=l&&k!=m&&k!=n&&l!=m&&l!=n&&m!=n&&a[0][i]+a[1][j]+a[2][k]+a[3][l]+a[4][m]+a[5][n]<=80)//较小的特殊值8+11+19+32+5+8=83{cout<"<>z;return0;}2、代码运行结果： 工厂生产过程调度一、问题重述图1是某企业的生产结构示意图，A是出厂产品，AA,,L,A是中间产品，图中0126kA⎯⎯⎯⎯→A表示生产一个单位A需k个单位A，其余类似。表1给出了生产单位产品所需的ijji资源(工人、设备)和时间，其中表中数据是基本的，即不能通过增加工人和设备来节约时间，也不能通过延长时间来减少工人和设备。A014A3A531A1223AA45A15图1生产结构示意图表1生产单位产品所需资源和时间产品AAAAAAA0123456需Ⅰ类工人71273437181817要Ⅱ类工人30181713121223的技术工人79077511资甲种设备（台）4304422源乙种设备（台）1310026加工时间6365522T1无资源浪费、连续均衡生产的最小生产规模是多少？相应的最短周期是多少？其中“无资源浪费”指在整个生产周期中没有闲置的设备和闲散人员，“连续”指整个周期中所有产品的生产过程不会停顿，“均衡”指所有中间产品A,L,A的库存与上一周期结束时的16库存相同.“生产规模”是指完成整个生产过程所需各资源的总和.T2如果考虑相同的资源可以通用，那么问题1得到的最小生产规模在无资源浪费，均衡生产中能否减少.请写出你得到的生产规模，相应的周期和生产过程的调度方案.T3如果该企业的资源限制为：Ⅰ类工人120名，Ⅱ类工人80名，技术人员25名，甲 种设备8台，乙种设备10台，及周期限制（一星期，共24*5.5=132小时）.请你做出生产过程的调度方案，使在均衡生产条件下资源的浪费最小.二、符号说明（问题1）矩阵S表示生产单位产品所需的各类资源，矩阵中的每一列Z表示生产单位A所需ijjj要的各类资源的数量。⎡71273437181817⎤⎢⎥30181713121223⎢⎥S=⎢79077511⎥ij⎢⎥⎢4304422⎥⎢⎣1310026⎥⎦T表示生产周期。k表示资源不可通用时用于生产A的资源向量Z的套数。jjjt为加工单位A所需的时间。jjP表示一个周期内A的产量。jj（问题2）nnnnn,,,,分别表示资源可以通用时I类工人、II类工人、技术工人、甲种设01234备及乙种设备的数量。Bj=[1,4,5,6,15,12,12](j=0⋯6)表示均衡生产时各种产品满足的比例。（问题三）W表示资源浪费指标。ft表示第i个资源在一周期内闲散或闲置的时间。iBe表示A开始生产的时刻，St表示A生产结束的时刻。jjjj三、模型假设1、生产规模指完成整个生产过程中所需各资源的总和。2、工人和设备都能连续工作，并且工作效率保持不变。3、开始时中间产品的库存量足够，各类产品的生产能够同时开工且不会因缺少中间产品而引起生产中断。4、单位产品的生产必须是连续的。5、忽略各中间产品在各个生产环节之间的输送时间6、生产单位产品的过程中，资源和时间应该按表1给出的基本量投入，工人和设备始 终要投入工作。7、T1中不考虑资源的通用，T2和T3中相同的资源在时间不冲突的情况下可以通用，忽略资源在两种产品之间进行转换的时间。8、各类资源数及周期数（以小时为单位）均为正整数。四、模型的建立与求解问题1：问题分析：由于我们假设相同的资源是不可以通用的，所以对于每种产品都对应着自己的一套独立的资源Z。j在这种情况下，题目中的“均衡”和“连续”是两个十分苛刻的条件。因为均衡要求所有中间产品的库存量与上一周期结束时相同，即在一个周期之中任一中间产品的生产量和消耗量必须严格相等；而连续要求整个周期中所有产品的生产过程不会停顿。这样就会带来一对矛盾，因为对题目稍加分析之后就会发现要满足“均衡”的条件A,L,A必须满足比例1:4:5:6:15:12:12；而要满足“连续”的条件A,L,A06061111111必须满足另一比例关系::::::。这显然是不能同时满足的。6365522解决的思路就是增加生产各种产品所需资源Z的套数，以求在相同的时间内生产更多j的某种产品，从而使在相同的时间内生产的各种产品能满足1:4:5:6:15:12:12的比例。问题的求解：由于生产单位不同产品所用的时间不同，生产周期必为tLt的整数倍。因为我们要06求其最小生产规模和最短生产周期所以不妨先取T等于其最小公倍数30。这样在一个周期内A的产量P就可以表示为jjTP=kjj。tj即P=5k、P=10k、P=5k、P=6k、P=6k、P=15k、P=15k。00112233445566又由生产结构示意图以及均衡生产的条件可知，每生产一单位A就必须生产4单位A、015单位A、6单位A、15单位A、12单位A、12单位A。从而PLP满足比例关系2345606 1:4:5:6:15:12:12，于是有5k10k5k6k6k15k15k0=1=2=3=4=5=6=λ。1456151212要求kLk为尽可能小的整数。取λ=10，则06k=2、k=4、k=10、k=10、k=25、k=8、k=8。从而最小的0123456产量规模为P=(5,10,5,6,6,15,15)kkkkkkkj0123456=(10,40,50,60,150,120,120)对应的各类资源的数量为：6ni=∑kj×Sijj=0解得：n=1690、n=1012、n=423、n=192、n=8801234，对应的最短周期为30h。问题2：问题分析：第二问考虑相同的资源可以通用，同时放弃了“连续生产”的条件。这两点无疑使得生产的调度方案更加灵活，因为对某个工人和设备来说在一个周期内可以一会儿生产这个一会儿又去生产那个。并且对每种产品来说也不用自始至终都在生产线上。但均衡生产和无资源浪费的要求是没有改变的。即所有产品ALA依然要满足061:4:5:6:15:12:12的比例关系，并且所有工人和设备在一个周期内自始至终都在工作。问题的求解：基于上面的考虑，对某个工人或设备来说他（它）在一个周期内都生产了些什么东西已经不再是确定的。那我们如何衡量工人和设备所干活儿的量呢？我们引入工数的概念:G=n×t令工数ii表示n单位的第i类资源在时间t内所干活儿的量。这样定义显然是合理的，因为在资源i 数量固定的情况下时间加倍必然导致产出加倍、时间一定的情况下资源数量加倍也必将导致产出的加倍。况且实际生活中确实有这样的实例和类似于“工数”的概念。于是当一个周期内有m个A0产出时，对每一种资源（包括各类工人和设备）在一个周期T内可以得到一个工数方程：6ni×T=m×∑Sij×Bj×tjj=0即有如下方程组：n×T=m×(7116274334563765181551812217122)××+××+××+××+××+××+××0n×T=m×(3016184317561365121551212223122)××+××+××+××+××+××+××1n×T=m×(7169430567657155512211122)××+××+××+××+××+××+××2n×T=m×(416343056465415521222122)××+××+××+××+××+××+××3n×T=m×××+××+××+××+×(116343156065015521226122)×+××+××4化简得：mn=5070×0Tmn=3036×1Tmn=1269×2Tmn=576×3Tmn=264×4T其中T表示周期长度，m表示一个周期加工A0的个数，n0Ln4分别表示一个周期内投入各类资源的数目。显然m和n0Ln4都必须为整数，且按照我们的约定T也为整数。要达到生产规模的最小即n0Ln4都取最小值，只要使上述方程组的各系数都分别除以 m1它们的最大公约数即可。5070、3036、1269、576的、最大公约数为2643，从而取=T3得：n=1690、n=1012、n=423、n=192、n=8801234此即资源可以通用、无资源浪费、均衡生产下的最小规模。注意到此最小规模与第一问中的最小规模完全一致，说明第一问中算得的最小生产规模在资源可以通用的条件下不能再减小。而且由于问题二放松了要求，问题一中的调度方案肯定也符合问题二。即可以令k组资源Z自始至终一刻不停地生产A。jjj其中k=(2，4,10，10,25,8,8)j。进一步思考：为什么第二次求得的生产规模（1）会和第一问中求得的生产规模（2）完全一致呢？事实上，由于规模（1）已经满足了均衡生产的条件，所以如果有更优的方案（2）的话，生产规模（1）必定会是它的整数倍。因为更优的规模（2）同样要满足均衡生产的条件。然而我们在第一问中所求得的生产规模（1），也即：n=1690、n=1012、n=423、n=192、n=8801234其各分量根本不存在公约数（除1之外），于是自然就不存在更小的生产规模和方案。问题3：问题分析：问题三放弃了前两问中“无资源浪费的条件”，但同时也增加了不少限制条件。n≤1200n≤801n≤252n≤83n≤105T≤132上述约束条件不仅对各类工人和设备的数量有限制、而且对周期的长短也有限制。由于给出的各类资源的数量并不符合均衡生产的比例，所以在生产过程中肯定有一种资源成为整个环节的“瓶颈”。即当这种资源全负荷工作时，其它资源仍有闲散或闲置。因此减小资源浪费的关键就是找到限制整个生产的瓶颈资源，并让这种资源全负荷运作。然后在去优化其它资源的调度。 问题的求解：基于上面的想法，假设令第i种资源全负荷运作（其它资源充足），计算生产一个A所0需要的时间。全负荷运作的资源满足工数方程：6ni×Ti=∑Sij×Bj×tjj=0令n=120、n=80、n=25、n=8、n=10有：01234T=42.25、T=37.95、T=50.76、T=72、T=26.401234可见限制整个生产过程的“瓶颈”是第三种资源，即甲种设备。且由T=72可知，在题3目所给132小时内最多只能生产一个A，并相应地生产中间产品。即一个周期内的产出为：0P=k=(1,4,5,6,15,12,12)jj由于我们的目的是尽量减少闲散人员和闲置资源，于是需要在满足72≤T≤132的所有情况中寻求一种方案使得在完成生产任务的前提下做到资源浪费最少。然而上面的分析告诉我们一个周期内的产量已经是固定，因此我们只能通过尽量缩短周期来达到减少资源浪费的目的让我们再仔细观察一下各类资源的需求与约束条件：产品A0A1A2A3A4A5A6限制条件I类工人71273437181817120II类工人3018171312122380技术工人7907751125甲种设备43044228乙种设备1310026106365522132tj1456151212Bj1232241kjmax612或630或15或30或1575或3824或12或824StBe−jj10或6 由于考虑到各类约束条件，生产A时我们最多能够投入资源Z的套数为1、生产A时001最多投入的套数为2LL以此类推，若以k表示生产时A能够投入的资源向量Z的套jjj数，则容易得到：k=10k=1或21k=1或2或32k=1或23k=1或24k=1或2或3或45k=16进一步我们可以求得加工所用的时间，若以Be表示A开始生产的时刻，St表示A生产jjjj结束的时刻，则有：B×tjjSt−Be=jjkj计算结果如上表所示。基于上述分析，若通过编程实现kLk、BeLBe以及T的任意组合，然后利用约0606束条件筛选出可行方案。但是所谓的“资源浪费最少”又怎么去衡量呢？下面我们定义资源浪费指标：W=∑fti令i表示一个周期内的资源浪费状况，其中i取遍每一个资源，ft表示该资源在该周期内闲散i或闲置的时间。W越大表示资源浪费越严重，W越小表示资源浪费越少。这样我们就可以在可行方案中找出资源浪费最小的方案。然而上述思路可行性并不好，因为牵扯到多重循环嵌套，代码的运行效率很低；况且即便能够得到可行的方案，其中也不一定有最优解。这又是为什么呢？因为上面考虑的思路中生产每种产品时投入资源的套数是固定的（比如，若开始生产A时投入2台甲种设备，那5 么直到A生产完毕为止就只有这两台设备在生产A），而实际生产中的资源调度往往更加灵55活（比如一开始有两台设备生产A,但过了一段时间由于另外一种产品生产结束，有更多台5甲种设备投入到A的生产中来）。这样必然导致更加节约资源的调度方案。5资源的限制条件允许在某一时刻任两种产品同时生产。于是充分做好生产的衔接并随时注意利用闲散资源就能得到最短的生产时间，从而使资源浪费最少。得到的最优解如下所示：即在第1小时投入2套Z生产Z，同时投入1套Z生产A；在第39小时投入1套4422Z生产A，同时投入一套Z生产A；在第45小时投入2套Z生产A；在第51小时投入110055一套Z生产A；在第57小时投入1套Z生产A；在第75小时再投入一套Z到A的生产663333中去。直到第81小时生产结束。进一步的思考：对于题目中所给出的数据来看，若只能取T=132的话，那么整个周期的资源浪费指标就是一定的了。因为我们前面已经证明了一个周期内只能够生产一个A0及相应数目的其他产品，所以用不了多久生产任务就会完成了。而周期是固定的，所以只要生产任务完成了W的值也就确定了。这里我们把题目中的限制条件“周期限制（一星期，共24*5.5=132小时）”理解为T≤132，这样做显然是合情合理的。因为倘若该工作可以在5天内完成，我们就没有 必要把它拖到7天才完成。我们完全可以只让工人工作两天，然后把剩下的两天当作假期或者休息日。而且在这两天里设备不被视作“闲置”，工人当然也不被视作“闲散”。模型的评价。问题一、二两种模型比较资源不可通用下求解，要求无资源浪费，连续均衡生产的最小生产规模，“无资源浪费”指在整个生产周期中没有闲置的设备和闲散人员。“连续”指整个周期中所有产品生产过程不会停滞，这样的生产比较浪费机器，机器损坏程度大，易受损。但是生产的生产周期比较短，生产速度快，相同资源可通用下求解，一个生产周期中,当某种产品的产量达到一定数量时,该产品的生产可以暂时停顿,其工人,设备被调作它用,去生产其他的产品，这样机器可以间接休息休息，不易老坏。但是生产周期比较长，生产速度慢。问题3模型的评价此题给出资源限制，1类工人120名，2类工人80名，技术人员25名，甲种设备8台，乙种设备10台即周期（一周共24*5.5=132小时）下，仍是在相同资源可通用的前提下求解的，与问题2相同，解无资源浪费，均衡生产的最小生产规模，生产的最小周期和生产过程的调度方案，这样可以更好地资源调度，实现最大生产。本次建模的优点：1、严格按照要求地解决了题目中的问题，在问题2中，引入了工数的概念，为解决该问题提供了一个简便的方法。2、在本模型的求解过程中，很好的使用了制表、绘图等表现方式，表达更为清晰易懂；计算中使用C++、MATLAB等工具，使求解变得快捷精确。模型不足：1、问题1中模型太过理想化，在实际中很难达到问题所要求的条件。2、问题3中的限制条件与实际较为接近，但是亦不够完全，比如，可能不是每个工人都能掌握生产每一种零件的技术之类，在这方面，还可以提出更多假设以是问题更加实际化。